-其它- 几种常见的排序

冒泡排序

冒泡排序的原理总的来说就是小的浮上来，大的沉底。

思路：如果$ai < a{i+1}$，则交换。

原理示意图：

冒泡排序的平均情况时间复杂度为$O(n^2)​$。

代码如下：

void Bubble_Sort(int a[],int length) {
    for(int i=1; i<=n-1; i++) {
        int m=1;
        for(int j=1; j<=n-i; j++) {
            if(a[j]>a[j+1]) {
                m=0;
                temp=a[j];
                a[j]=a[j+1];
                a[j+1]=temp;
            }
        }
        if(m==1) break;
    }
}

快速排序

快排的思路是：先选取一个基准，然后将比基准小的放在左边，将比基准大的放在右边，然后再分小区间，重复以上操作。

原理示意图：

快速排序的平均情况时间复杂度为$O(n\log_2 n)​$。

代码：

void Quick_Sort(int s[], int l, int r) {
    if(l<r) {
        int low=l;
        int high=r;
        int pivot = s[l];
        while(low<high) {
            while(low<high&&s[high]>= pivot)
                high--;
            if(low<high)
                s[low++] = s[high];
            while(low<high&&s[low]<pivot)
                low++;
            if(low<high)
                s[high--] = s[low];
        }
        s[low]=pivot;
        QuickSort(s, l, low - 1);
        QuickSort(s, low + 1, r);
    }
}

插入排序

首先回忆一下你是怎么玩牌的，每次摸到一张牌，都要把它插入到正确位置。

插入排序的原理一样，首先查找一下它的正确位置$a_i$，然后将$a_i$后数向后移动一位，将这个数插入进去。

原理示意图：

插入排序的平均情况时间复杂度是$O(n^2)$。

代码：

void Insertion_Sort(int arr[],int length) {
    int i,j,key;
    for(i=0; i<length; i++) {
        key=arr[i];
        for(j=i-1; j>=0; j--) {
            if (arr[j]>key) {
                arr[j+1]=arr[j];
            } else {
                break;
            }
        }
        arr[j+1]=key;
    }
}

选择排序

选择排序原理：首先找出最小值，然后放在数列的最前面，如此反复。

原理示意图：

选择排序的平均情况时间复杂度为$O(n^2)$。

代码如下

void Selection_Sort(int a[],int length){
    for(int i=0;i<n;i++){
        int k=i;
        for(int j=i;j<n;j++){
            if(a[j]<a[k]){
                k=j;
            }
        }
        int t=a[i];
        a[i]=a[k];
        a[k]=t;
    }
}

桶排序

设一个数组为桶，数组的大小为待排序数列的最大值加1，桶号即为数列的每一个值，当出现这个数时，对应的桶就加1。

原理示意图：

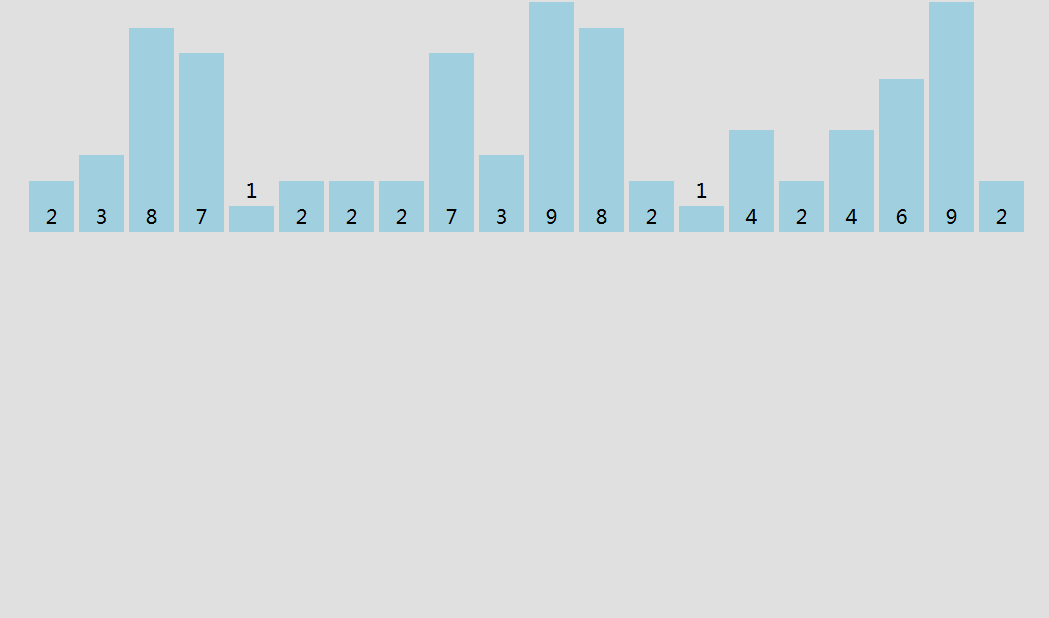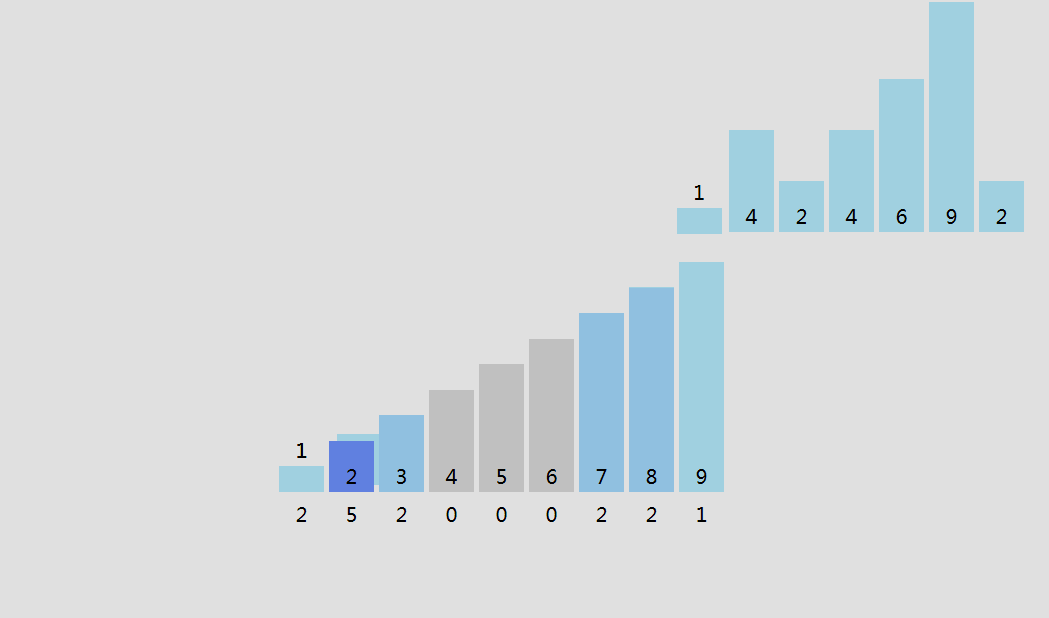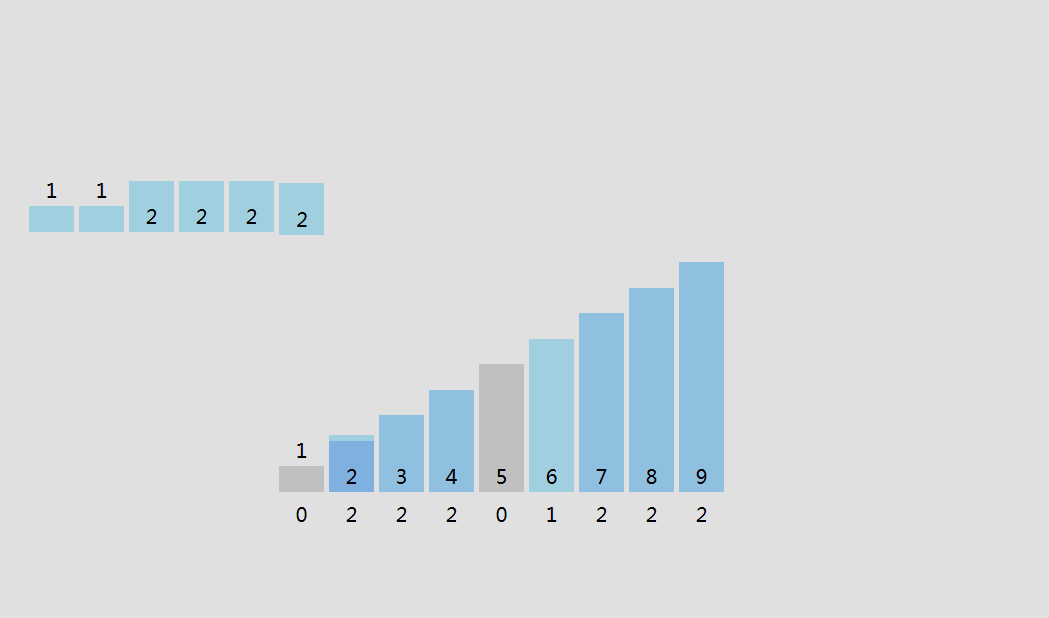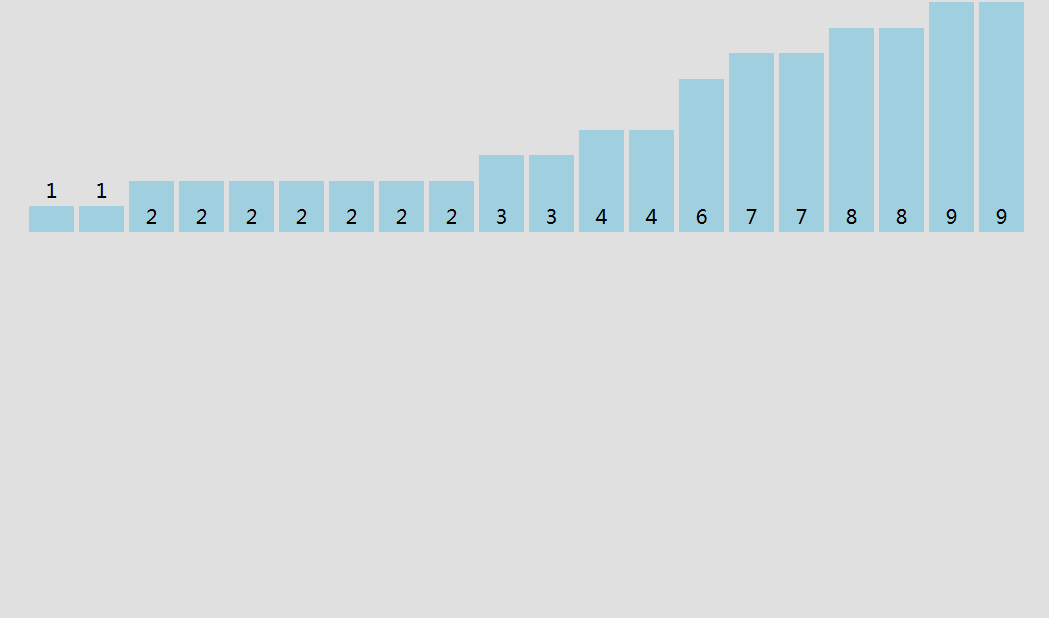
桶排序的平均情况时间复杂度为$O(n)$，但空间复杂度为$O(n)$。

代码：

void Bucket_Sort(int a[], int max, int length) {
    int B[max+1]= {0};
    int i,j,count=0;
    for (i=0; i<length; i++) {
        B[a[i]]+=1;
    }
    for(i=0; i<=max; i++) {
        if (B[i]>0) {
            for(j=0; j<B[i]; j++) {
                a[count]=i;
                count++;
            }
        }
    }
}

终极の排序

不需要任何算法，直接一个函数搞定！

sort(a+1,a+1+n)

别忘了加这个头文件：

#include<algorithm>

还可以通过写一个函数来决定从大到小排还是从小到大排。