题目描述
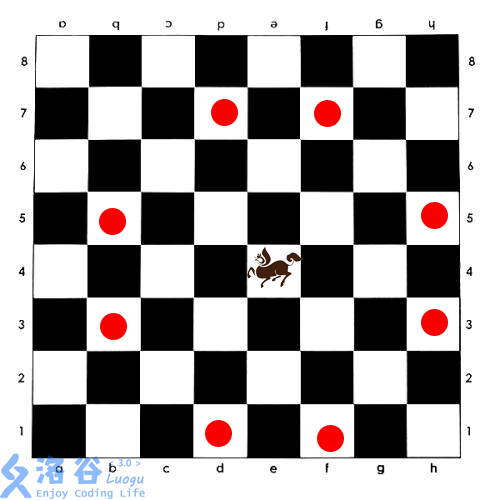
如图所示,西洋棋的“长脖子鹿”,类似于中国象棋的马,但按照“目”字攻击,且没有中国象棋“别马腿”的规则。(因为长脖子鹿没有马腿)
![]()
给定一个 $N * M$ ,的棋盘,有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。
输入格式
输入的第一行为两个正整数 $N$,$M$,$K$。其中 $K$ 表示禁止放置长脖子鹿的格子数。
第 $2$ ~第 $K+1$ 行每一行为两个整数 $Xi, Yi$,表示禁止放置的格子。
输出格式
一行一个正整数,表示最多能放置的长脖子鹿个数。
输入样例
8 7 5
1 1
5 4
2 3
4 7
8 3
输出样例
28
说明
重要提示:请务必思考对图的遍历顺序对运行速度的影响
对于 $10\%$ 的数据,$1 ≤ N,M ≤ 5$
对于 $30\%$ 的数据,$1 ≤ N,M ≤ 10$
对于 $60\%$ 的数据,$1 ≤ N,M ≤ 50$
对于 $80\%$ 的数据,$1 ≤ N,M ≤ 100$
对于 $100\%$的数据,$1 ≤ N,M ≤ 200$
Solution
这道题是一道求二分图最大独立集的题,只是需要改一下建图方式。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
| #include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define MAXN 1000010
namespace STman {
template <typename Tp>
inline void read(Tp &x) {
#define C getchar()
Tp f = 1;
x = 0;
char k = C;
while (k < '0' || k > '9') {
if (k == '-') f = -1;
k = C;
}
while (k >= '0' && k <= '9') {
x = x * 10 + k - '0';
k = C;
}
x = x * f;
#undef C
}
template <typename Tp>
inline void write(Tp x) {
if (x < 0) putchar('-') , x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
template <typename Tp>
inline Tp max(Tp a , Tp b) {
if (a > b) return a;
else return b;
}
template <typename Tp>
inline Tp min(Tp a , Tp b) {
if (a < b) return a;
else return b;
}
template <typename Tp>
inline void swap(Tp &a , Tp &b) {
Tp t = a;
a = b;
b = a;
}
template <typename Tp>
inline Tp abs(Tp &a) {
if (a < 0) return -a;
else return a;
}
inline void sp() {
putchar(32);
}
inline void et() {
putchar(10);
}
}
using namespace STman;
struct Edge {
int v, nx;
}e[MAXN];
int head[MAXN], ecnt, n, m, h, G[210][210], x, y, ans, tot, vis[MAXN], mtch[MAXN], cnt;
int dx[] = {0, -1, -3, 1, 3, -1, -3, 1, 3}, dy[] = {0, -3, -1, -3, -1, 3, 1, 3, 1};
int g(int i, int j) {
return (i - 1) * m + j;
}
void add(int f, int t) {
e[++ecnt] = (Edge) {t, head[f]};
head[f] = ecnt;
}
bool Hungary(int k, int t) {
for (int i = head[k]; i; i = e[i].nx) {
int to = e[i].v;
if (vis[to] != t) {
vis[to] = t;
if (!mtch[to] || Hungary(mtch[to], t)) {
mtch[to] = k;
return 1;
}
}
}
return 0;
}
int main() {
read(n), read(m), read(h);
for (int i = 1; i <= h; i++) {
read(x), read(y);
G[x][y] = 1;
}
for (int i = 1; i <= n; i += 2) {
for (int j = 1; j <= m; j++) {
if(!G[i][j]) {
for (int k = 1; k <= 8; k++) {
int tx = i + dx[k], ty = j + dy[k];
if (tx > n || tx < 1 || ty > m || ty < 1 || G[tx][ty]) continue;
add(g(i, j), g(tx, ty));
}
}
}
}
for (int i = 1; i <= n; i += 2) {
for (int j = 1; j <= m; j++) {
if (!G[i][j]) {
if (Hungary(g(i, j), ++cnt)) {
ans++;
}
}
}
}
write(n * m - h - ans);
return 0;
}
|