如果有个题目,要求你在数列上区间求和,支持修改。
那么这道题就是很简单的线段树板子题,对吧?
但是,这个世界是残酷的。为了不让题目那么简单,邪恶的出题人会把序列上的转换到树上,使题目难度增加一倍甚至几倍。
这样一看,完了,线段树可处理不了树上的操作啊,顿时感到人生苦短,失去了活下去的勇气。
那么,一个神奇的而又强大的东西——树链剖分可以解决上述问题。
前置知识:DFS序、线段树。
啥,你不会线段树?序列上的问题都不会处理就想处理树上的问题?你快醒醒!
变量的定义(当然这都是根据个人喜好来定义变量的名称,但作用都是一样的):
1 | int dep[MAXN]; // 每个节点的深度 |
下面进入正题:
让我们先来看这幅图:
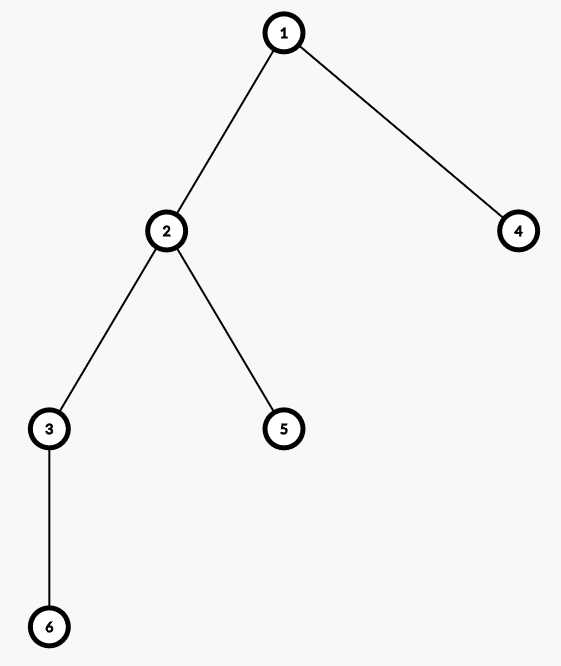
显然这是一棵树。
那么我们该如何处理这棵树使它能够转换为序列上的问题呢。
我们可以把这棵树剖分一下,剖分成一些不同的链,分为重链和轻链。
什么是重链?就是把重儿子连在一起形成的链。
所以轻链也就是把轻儿子连在一起形成的链。
那什么又是重儿子呢?就是在一个节点的所有儿子中,子树最大的那个。当然,可能会出现具有相同大小子树的情况,我们只需要任选一个就行了。
轻儿子就是就是一个节点除重儿子外的所有儿子
还是这棵树:
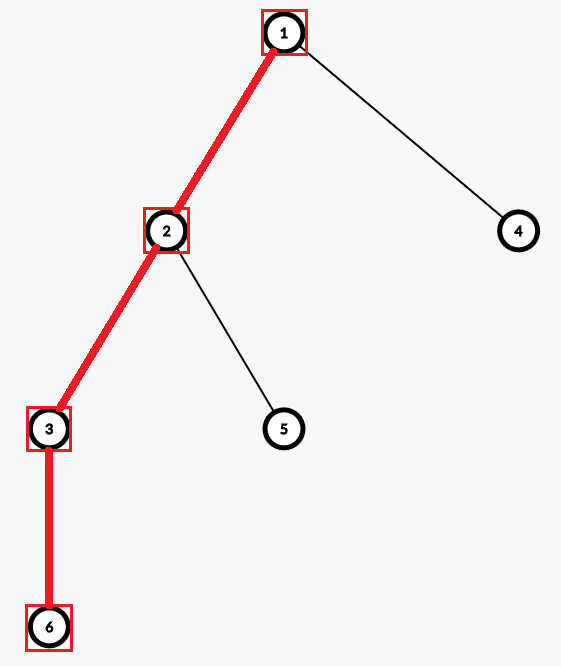
上图已经用红线标出了所有重链,红色正方形的节点是重儿子,为了方便处理,我们把根节点也算作重儿子。
现在问题来了,该如何求出重儿子、轻儿子、重链、轻链呢?
下面放程序:
1 | void dfs1(int u, int f, int deep) { |
是不是很巧妙?好像不是一个dfs就解决完轻重儿子的问题,下面再来个dfs来解决轻重链的问题:
1 | void dfs2(int u, int topf) { |
更为巧妙的是,上面这个程序保证每条链内的标号是连续的
至此,树链剖分结束
等一下,已经把这棵树处理完了,该如何用树链剖分解决树上的操作呢。
处理树上的操作分为三个问题:
1.单点的操作
直接线段树单点修改就行了。
2.子树的操作
让我们回忆一下DFS序的过程:每次都是搜到底再回溯。
所以我们可以得出一条结论:在子树中,每个节点的标号是连续的。
然后用线段区间修改就行了
3.路径上的操作
这才是重点所在,树链剖分就是擅长处理这种操作!
我们既然已经划分出轻重链了,那么我们现在同等对待他们。
先给出程序:
1 | inline void query(int x, int y) { |
别看这程序短小,但这是树链剖分的精华所在!浓缩的都是精华
下面开始解读程序
while (top[x] != top[y])这句是什么意思呢?
如果这两个点不在一条链上,那就不断跳,知道跳到同一条链上为止。
if (dep[top[x]] < dep[top[y]]) swap(x, y);这又是什么意思呢?
还是这张图:

如果我们要处理从节点6到节点5的操作,会发现节点5所在链的顶端正好与节点6所在链的中间相连。
如果我们不加上面这句话,很可能就会跳到其它无关紧要的节点上,并且陷入死循环。
if (dep[x] > dep[y]) swap(x, y); 这句话就是为了处理当x,y跳到了同一条链上的时候该如何处理(也就是求出两点的LCA)。
于是我们也可以上述程序写出求LCA的程序:
1 | inline int LCA(int x, int y) { |
最后,说一些关于树链剖分时间复杂度的问题。
树链剖分的复杂度真的很优秀,查询一次最坏复杂度是 $\log n$,而大多数情况下跑不满。同机房的Juan_feng对树链剖分的时间复杂度做出了证明:
任何一个点到根节点至多经过$\log$条轻边。
因为每个点如果经过一条轻边走向他的父亲,那么他的父亲的siz就至少是这个节点的2倍,所以最多经过log条轻边
终于,树链剖分完毕!
下面是几道例题:




