如果需要维护一个集合的最大值,那么我们可以直接用普通的堆来实现就行了。
但如果我们要维护多个集合的最大值,而且还要支持集合的合并操作,这时候就需要用可并堆来维护了。
为了方便说明,一下的操作都是以小根堆为基础进行。
可并堆有很多种,我选择了比较优秀的配对堆。
配对堆的核心操作就是合并。
那么该如何合并呢,比较两个堆的堆顶大小,大的合并到小的上面就行了。
其他常用的操作:
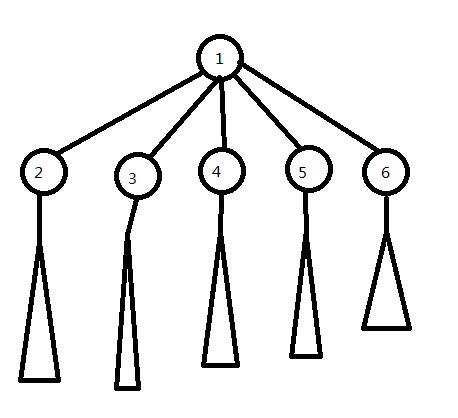
由于弹出最值操作非常抽象,所以我画了个图:
最初是情况下是这样的:
![]()
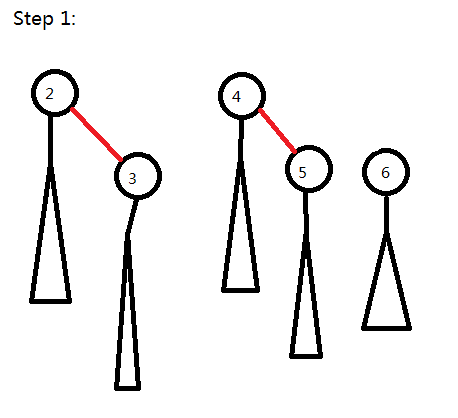
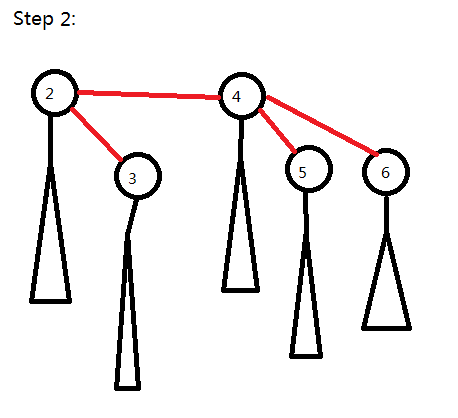
然后经过下面两个步骤:
![]()
![]()
这样就保证了复杂度的正确性。
最后摆出个借鉴抄别人的配对堆模板代码(强行增加文章长度):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1000010
struct Heap {
int v, id;
int s, xd;
}h[MAXN];
int fa[MAXN], a[MAXN];
bool ifd[MAXN];
int merge(int a, int b) {
if (h[a].v == 0) return b;
if (h[b].v == 0) return a;
if (h[a].v > h[b].v || (h[a].v == h[b].v && a > b)) std::swap(a, b);
h[b].xd = h[a].s;
h[a].s = b;
return a;
}
int merges(int a) {
if (h[a].v == 0 || h[h[a].xd].v == 0) return a;
int p = h[a].xd, q = h[p].xd;
h[a].xd = h[p].xd = 0;
return merge(merge(a, p), merges(q));
}
int del(int a) {
printf("%d\n", h[a].v);
h[a].v = -1;
return merges(h[a].s);
}
int find(int x) {
if (fa[x] == x) return x;
else return fa[x] = find(fa[x]);
}
bool un(int x, int y) {
if (x == y) return 0;
fa[y] = x;
return 1;
}
int head[MAXN], op, x, y, n, m;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
fa[i] = i;
}
h[0].v = 0;
for (int i = 1; i <= n; i++) {
head[i] = i;
h[i].v = a[i];
h[i].id = i;
h[i].s = h[i].xd = 0;
}
while (m--) {
scanf("%d", &op);
if (op == 1) {
scanf("%d%d", &x, &y);
int _x = find(x), _y = find(y);
if (ifd[x] || ifd[y] || !un(_x, _y)) continue;
head[_x] = merge(head[_x], head[_y]);
}
else {
scanf("%d", &x);
if (ifd[x]) {
puts("-1");
continue;
}
int _x = find(x);
ifd[h[head[_x]].id] = 1;
head[_x] = del(head[_x]);
}
}
}
|