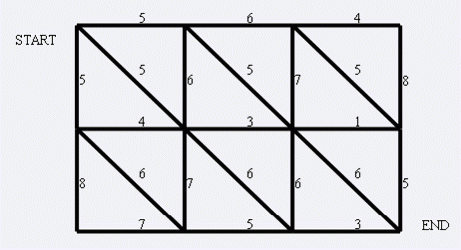
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
| #include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define MAXN 10000100
#define INF 2000000000
namespace STman {
inline char gc(){
#ifdef ONLINE_JUDGE
static char now[1 << 16], *S, *T;
if (T == S) {T = (S = now) + fread(now, 1, 1 << 16, stdin); if (T == S) return EOF;}
return *S++;
#else
return getchar();
#endif
}
template <typename Tp>
inline void read(Tp &x) {
Tp f = 1;x = 0;
char k = gc();
while (k < '0' || k > '9') {if (k == '-') f = -1;k = gc();}
while (k >= '0' && k <= '9') {x = x * 10 + k - '0';k = gc();}
x = x * f;
}
template <typename Tp>
inline void write(Tp x) {
if (x < 0) putchar('-') , x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
template <typename Tp>
inline Tp max(Tp a , Tp b) {
if (a > b) return a;
else return b;
}
template <typename Tp>
inline Tp min(Tp a , Tp b) {
if (a < b) return a;
else return b;
}
template <typename Tp>
inline void swap(Tp &a , Tp &b) {
Tp t = a;
a = b;
b = t;
}
template <typename Tp>
inline Tp abs(Tp &a) {
if (a < 0) return -a;
else return a;
}
inline void sp() {
putchar(32);
}
inline void et() {
putchar(10);
}
}
using namespace STman;
struct Edge {
int v, nx, w;
}e[MAXN];
std::queue <int> q;
int head[MAXN], ecnt = 1, n, m, x, dep[MAXN], cur[MAXN], r, k;
inline int g(int i, int j) {
return (i - 1) * m + j;
}
void add(int f, int t, int w) {
e[++ecnt] = (Edge) {t, head[f], w};
head[f] = ecnt;
e[++ecnt] = (Edge) {f, head[t], w};
head[t] = ecnt;
}
inline bool bfs(int s, int t) {
memset(dep, 0, sizeof(dep));
while (!q.empty()) q.pop();
for (int i = 1; i <= n * m; i++) {
cur[i] = head[i];
}
dep[s] = 1;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int i = head[v]; i; i = e[i].nx) {
int to = e[i].v;
if (dep[to] == 0 && e[i].w > 0) {
dep[to] = dep[v] + 1;
q.push(to);
}
}
}
if (dep[t] > 0) return 1;
else return 0;
}
int dfs(int u, int t, int l) {
if (!l || u == t) return l;
int fl = 0 , f;
for (int i = cur[u]; i; i = e[i].nx) {
cur[u] = i;
int to = e[i].v;
if (dep[to] == dep[u] + 1 && (f = dfs(to, t, min(l, e[i].w)))) {
fl += f;
l -= f;
e[i ^ 1].w += f;
e[i].w -= f;
if (!l) break;
}
}
return fl;
}
int Dinic(int s , int t) {
int maxf = 0;
while (bfs(s , t)) {
maxf += dfs(s , t , INF);
}
return maxf;
}
int main() {
read(n), read(m);
r = g(1, 1);
k = g(n, m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j < m; j++) {
read(x);
add(g(i, j), g(i, j + 1), x);
}
}
for (int i = 1; i < n; i++) {
for (int j = 1; j <= m; j++) {
read(x);
add(g(i, j), g(i + 1, j), x);
}
}
for (int i = 1; i < n; i++) {
for (int j = 1; j < m; j++) {
read(x);
add(g(i, j), g(i + 1, j + 1), x);
}
}
write(Dinic(r, k));
return 0;
}
|